Позор современной науке! Исламские ученые 14 века переплюнули современных учёных. Мы наивно полагали, что продвинутая математика и кристаллография – достижения сегодняшних дней. Оказывается, ничего подобного – всё это было уже семь веков назад. К тому же современную науку, похоже, перегнали не математики, а простые художники. Ну, может, и не очень простые…

    Нет, ну в самом деле — современные математики занимаются сплошной ерундой! То бумагу складывают по 12 раз, то вяжут крючком уравнения Лоренца, то выкручивают мячики в пончики.

    А ведь интересно, что математические достижения люди совершали и в древности, порой совершенно не придавая им особенного значения. Занятно также, что те же "старинные" открытия учёные повторяют в наши дни, ничуть при этом не подозревая, что выдумывают нечто, существующее без их догадок не одно столетие.

    Вот, скажем, английский математик Роджер Пенроуз (Roger Penrose) придумал в 1973 году такую штуку – особенную мозаику из геометрических фигур. Называться она стала, соответственно, мозаикой Пенроуза. Чего же в ней такого специфического?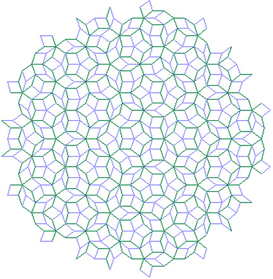

    Мозаика Пенроуза представляет собой узор, собранный из многоугольных плиток двух определённых форм (немного различающихся ромбов). Ими можно замостить бесконечную плоскость без пробелов.

    Получающееся изображение выглядит так, будто является неким "ритмическим" орнаментом – картинкой, обладающей трансляционной симметрией. Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно "копировать" на плоскости, а затем совмещать эти "дубликаты" друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).
Однако, если присмотреться, можно узреть, что в узоре Пенроуза нет таких повторяющихся структур – он апериодичен. Но дело отнюдь не в оптическом обмане, а в том, что мозаика не хаотична: она обладает вращательной симметрией пятого порядка.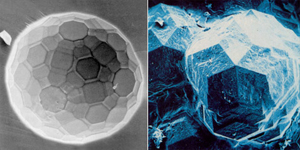

    Это значит, что изображение можно поворачивать на минимальный угол, равный 360 / n градусам, где n – порядок симметрии, в данном случае n = 5. Следовательно, угол поворота, который ничего не меняет, должен быть кратен 360 / 5 = 72 градусам.

    Примерно десятилетие выдумка Пенроуза считалась не более чем милой математической абстракцией. Однако в 1984 году Дэн Шехтман (Dan Shechtman), профессор израильского технологического института (Technion), занимаясь изучением строения алюминиево-магниевого сплава, обнаружил, что на атомной решётке этого вещества происходит дифракция.

    Предыдущие представления, существовавшие в физике твёрдого тела, исключали такую возможность: структура дифракционной картины обладает симметрией пятого порядка. Её части нельзя совмещать параллельным переносом, а значит, это вовсе никакой не кристалл. Но дифракция характерна как раз для кристаллической решётки!

    Как тут быть? Вопрос непростой, поэтому учёные договорились о том, что данный вариант будет назваться квазикристаллами – чем-то вроде особого состояния вещества.

    Ну а вся красота открытия, как вы догадались, в том, что для него уже давно готова математическая модель. И, как вы наверное поняли, это мозаика Пенроуза. Вот только ей этой вовсе не десять лет, а гораздо больше. Это стало известно лишь в наши дни, на заре XXI века, и модель эта оказалась намного древнее, чем можно было себе представить.

    В 2007 году Питер Лу (Peter J. Lu), физик из Гарварда (Harvard University) за компанию с другим физиком — Полом Стейнхардтом (Paul J. Steinhardt), но из Принстона (Princeton University), — опубликовал в Science статью, посвящённую мозаикам Пенроуза. Казалось бы, неожиданного тут немного: открытие квазикристаллов привлекло живой интерес к данной теме, что привело к появлению кучи публикаций в научной прессе.

    Однако изюминка работы в том, что она посвящена далеко не современной науке. Да и вообще — не науке.

    Лу обратил внимание на узоры, покрывающие мечети в Азии, построенные ещё в Средневековье. Эти легко узнаваемые рисунки сделаны из мозаичной плитки. Они называются гирихи (от арабского слова "узел") и представляют собой геометрический орнамент, характерный для исламского искусства и состоящий из многоугольных фигур.

    Долгое время считалось, что эти узоры создавались с помощью линейки и циркуля. Однако пару лет назад, находясь во время путешествия в Узбекистане, Лу заинтересовался узорами мозаик, украшавшими местную средневековую архитектуру, и приметил в них что-то знакомое.

    Вернувшись в Гарвард, учёный стал рассматривать аналогичные мотивы в мозаиках на стенах средневековых построек Афганистана, Ирана, Ирака и Турции.

    Он обнаружил, что эти схемы практически одинаковы, и смог выделить основные элементы гирихов, использовавшихся во всех геометрических орнаментах. Кроме того, он нашёл чертежи этих изображений в старинных манускриптах, которыми древние художники пользовались в качестве своеобразной шпаргалки по украшению стен.

    Но это всё, оказывается, не так уж важно. Для создания этих узоров применяли не простые, случайно придуманные контуры, а фигуры, которые были расположены в определённом порядке. И это не особенно удивительно.
А действительно интересно то, что, забыв про подобные схемы, люди снова встретились с ними позже. Да-да, древние узоры – не что иное, как то, что спустя столетия назовут решётками Пенроуза и найдут в структуре квазикристаллов!

    В исламской традиции большую популярность приобрёл геометрический орнамент. Средневековые мастера умудрялись как-то делать его разнообразным. Но в чём был секрет их "стратегии" – никто не знал. Так вот, секрет как раз оказывается в использовании специальных мозаик, которые могут, оставаясь симметричными, заполнять плоскость, не повторяясь.

    Другой "фокус" этих изображений в том, что, "копируя" такие схемы в различных храмах по чертежам, художники неизбежно должны были бы допустить искажения. Но нарушения данного характера минимальны. Объясняется это только тем, что в масштабных чертежах смысла не была: главное – принцип, по которому строить картину.

    Для сборки гирихов применяли плитки пяти видов (десяти— и пятиугольные ромбы и "бабочки"), которые в мозаике составлялись, прилегая друг к другу без свободного пространства между ними. Мозаики созданные из них, могли обладать как сразу вращательной и трансляционной симметрией, так и только вращательной симметрией пятого порядка (то есть являлись мозаиками Пенроуза).

    Исследовав сотни фотографий средневековых мусульманских достопримечательностей, Лу со Стейнхардтом смогли датировать появление подобной тенденции XIII веком. Постепенно этот способ приобретал всё большую популярность и к XV веку стал широко распространённым.

    Образцом почти идеальной квазикристаллической структуры исследователи посчитали архитектурный комплекс Дарб-и в иранском городе Исфахане, датируемое 1453 годом.

    Это открытие впечатлило очень многих. Американская ассоциация содействия развитию науки (AAAS) на радостях подготовила по этому случаю пресс-релизы, посвящённые исследованию, даже на персидском, арабском и турецком языках (видимо, в качестве "дани" за вдохновение).

    Правда, доктор Эмиль Маковицкий (Emil Makovicky) из Копенгагенского университета (University of Copenhagen) посчитал своим долгом пожурить исследователей за то, что они недостаточно уделили внимания его статье 1991 года, в которой он исследовал узор на одном мавзолее XII века. Вскоре к этой критике присоединилась ещё пара учёных — из Technion и из университета Дюка (Duke University), сказав, правда, что работа Стейнхардта и Лу представляет собой "интересную гипотезу".

    Пол Стейнхардт честно парировал замечание, сказав, что он с коллегой работал не над одним образцом, а над большим количеством разнообразного материала. К счастью, до академической ссоры дело не дошло, а исследование получило хоть какое-то признание в научном мире.

    И всё же самый таинственный вопрос – о том, как средневековые арабы могли додуматься до квазикристаллических структур, которые известны нам менее трёх десятилетий, — так и остаётся без ответа.

    Может ли это быть доказательством огромной роли математики в средневековом исламском искусстве, или это просто был наиболее простой способ "сборки" авторами своих произведений – сейчас узнать уже невозможно.

    "Мы не можем с уверенностью сказать, что означает всё это искусство, — признался Питер Лу. — Однако кажется невероятным, что выбор такой тактики – дело простой случайности". В любом случае это открытие может быть свидетельством того, что искусство, которому не придают большого значения, оказалось куда более "продвинутым", чем мы могли предположить.